Three Steps to Understand Symmetry in Crystallography
Symmetry in an object, and even more in a crystal, can be hard to visualize and understand.
In this blog we provide a three-step approach for chemistry students to understand symmetry in crystallography and highlight resources and tools to help you visualize symmetry in molecules and crystals.
As a charity, one of our key missions is education in the chemical sciences. We do that by offering teaching and learning resources like this blog, and many more that can be accessed on our Training and Learning and Education and Outreach pages.
Our education newsletter brings the latest resources straight to you – sign up here.
1. Symmetry in Molecules
Symmetry is the ability of an object to appear unchanged after undergoing a certain type of movement. In crystallography, these movements are called symmetry operations.
The first step to understand symmetry in crystallography is to visualize and recognize symmetry operations on molecules.
If we look at a molecule of water, we can imagine an axis running through the atom of oxygen (coloured in red) like in Figure 1. With a rotation of 180° around this axis, the molecule of water appears unchanged. Note that “unchanged” means that there is no way to distinguish the initial object from the final object. Hence, this rotation is an example of a symmetry operation for the molecule of water.
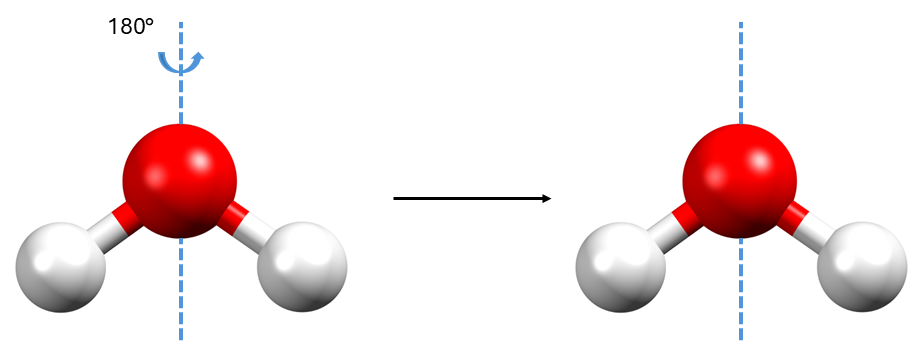
To perform the 180° rotation of the molecule of water, we had to introduce the rotation axis that can be seen in Figure 1: this is called a symmetry element.
A symmetry element is a geometrical entity about which a symmetry operation is performed, such as a point, an axis, or a plane.
Now that key concepts of symmetry have been introduced, we can list the symmetry operations of molecules:
- Rotation, indicated with Cn, where n is the number of rotations that fit in 360°; it takes place when a molecule is rotated around a n-fold rotation axis;
- Reflection, indicated with σ; it takes place when a molecule is reflected with respect to a mirror plane; if the mirror plane includes the principal rotation axis this is called σv (vertical); if it is perpendicular to the axis, it is called σh (horizontal); if a vertical mirror plane bisects the angle between two C2 axes it is called σd (dihedral);
- Inversion, indicated with i; it transforms the coordinates of point (x, y, x) to (-x, -y, -z), and consists of passing each point through the centre of inversion of the molecule, and out to the same distance from the centre on the other side of the molecule;
- Improper rotation, indicated with Sn; it consists of a Cn rotation followed by a reflection in a plane perpendicular to the axis;
- Identity, indicated with E; this operator is peculiar as it leaves the object the way it is, but is essential for the mathematical description of point groups and symmetry.
What Are Point Groups?
Molecules of different shapes can differ in the number and type of symmetry operations that they can undergo. Despite this, there is a limited number of possible combinations of symmetry operations that can be applied to molecules: these are called point groups and are defined as the complete set of symmetry operations that leave at least one point of an object unmoved.
For a molecule of water, for example, we can identify the following symmetry operations (Figure 2):
- Identity, E, present in all the molecules;
- Rotation, C2, with a twofold rotation axis;
- Two reflections, σv, with a mirror plane coincident to the plane where the water molecule lies and one perpendicular to the latter.
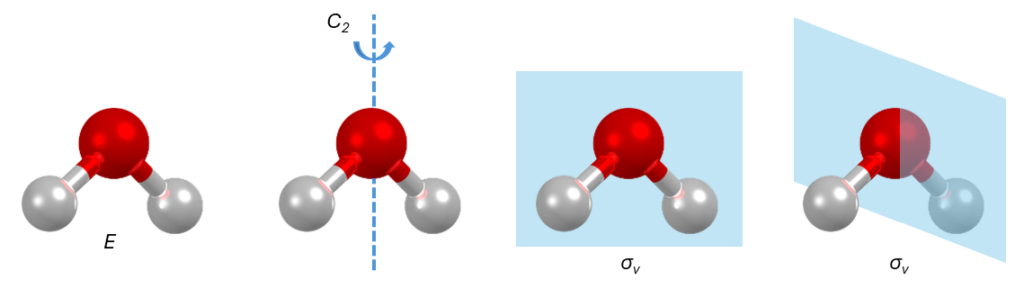
The combination of these four symmetry operations forms a specific point group that is hence assigned to water: C2v. This means that even molecules that are chemically different can be part of the same point group, as this describes the symmetry operations that they can undergo.
Other examples of simple molecules with the same point group as water are formaldehyde, pyridine, and acetone (Figure 3): can you spot the same four symmetry operations listed for water?
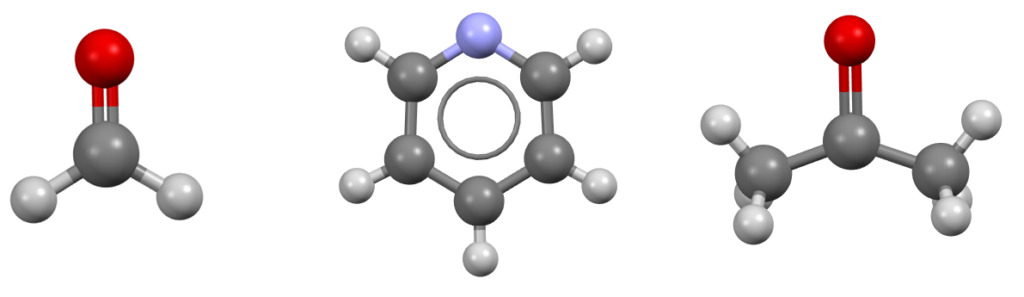
If you are now wondering how to assign a point group to a given molecule, we have two excellent resources that can help you with that:
- Our video “Introduction to Symmetry Operations and Point Groups”, which guides you through the basics of point groups with examples that demonstrate the effects of symmetry operations on molecules;
- Our flowchart to determine point groups included in our teaching module on symmetry, that you can use to identify which point group should be assigned to a molecule.
2. Symmetry in Crystals
Now that the symmetry operations in simple molecules are clear, we can move to understanding symmetry in crystals, where single molecules are packed together in repeating patterns.
Symmetry in crystals is treated in a similar way to that of molecules. In fact, crystals also have the symmetry elements found in molecules: mirror planes, rotation axes, centres of inversion, and improper rotation axes (Figure 4, from top to bottom).
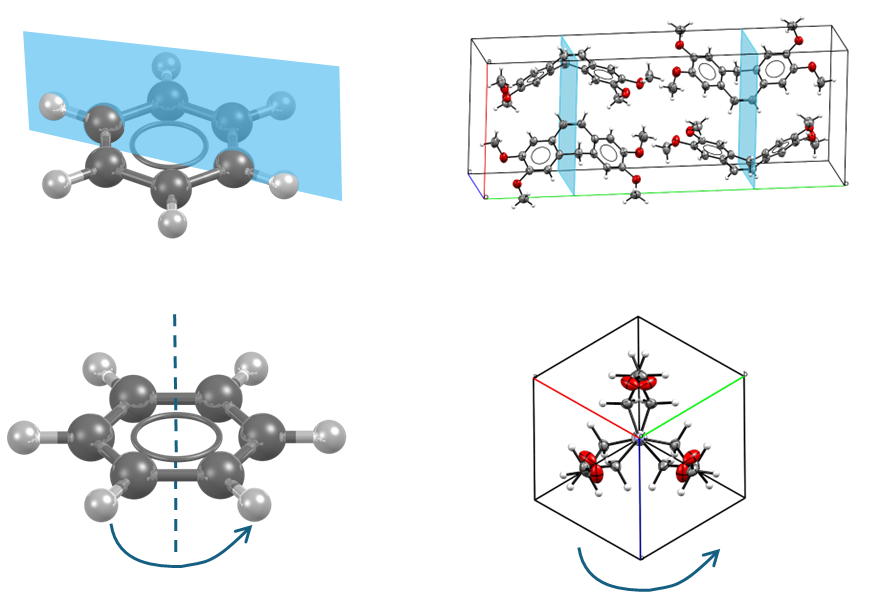
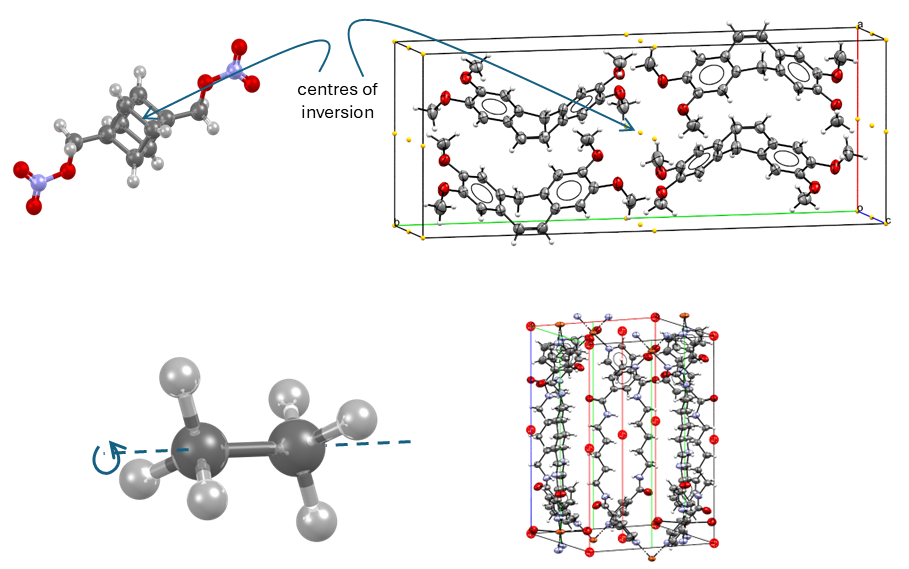
The main difference between molecules and crystals is that a periodic 3D structure also allows symmetry operations that involve translational elements. The two additional symmetry elements for crystals are screw axes and glide planes.
To better understand what screw axes look like, you should:
- Know that the symmetry operation that involves a screw axis, called screw rotation, consists of a rotation around an axis, followed by a translation parallel to that axis;
- Look at some examples highlighted in the video “Introduction to symmetry operations and symmetry elements: screw axis”, where you will also learn the nomenclature of screw axes.
Then, to better understand what glide planes look like, you should:
- Know that the symmetry operation that involves a glide plane, called glide reflection, consists of a reflection through a plane, followed by a translation parallel to that plane;
- Look at some examples highlighted in the video “Introduction to symmetry operations and symmetry elements: glide reflections”.
It should be noted that whilst a molecule considered in isolation could in theory adopt any point group, only certain point groups are compatible with the translational symmetry of a crystal. There are in fact only 32 possible crystallographic point groups.
Point Groups vs Space Groups
As mentioned above, all the symmetry operations included in a point group leave at least one point of the object unmoved. This means that all the symmetry elements in a single molecule pass through one point.
The symmetry elements in a crystalline solid, instead, do not all pass through one point, but they are regularly arranged in the space.
The total number of possible arrangements of symmetry elements in the crystalline solid state is exactly 230, and the symmetry group of a three-dimensional crystal pattern is called its space group.
3. Using Mercury to Visualize Symmetry
Our software Mercury can help you visualize and analyse molecular structures and their properties, including symmetry elements.
Visualizing symmetry elements in Mercury is very easy (Figure 5):
- Open Mercury and type a CSD refcode of interest on the “Structure Navigator” bar (top right); for this example, we will use the CSD refcode: JAGREP;
- Go to “Display” > “Symmetry Elements”.
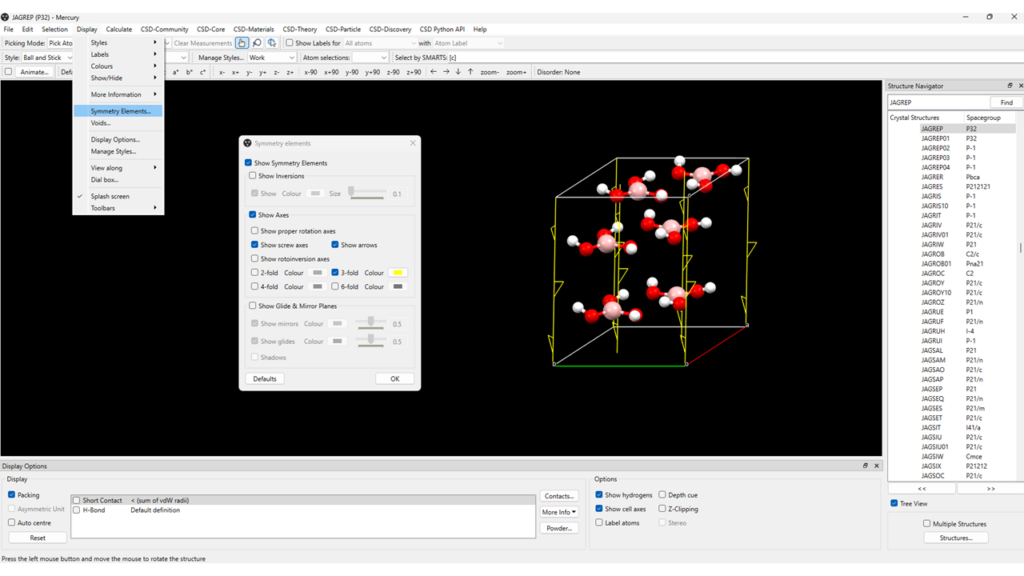
Displaying the packing of the molecules can help you visualize the symmetry elements in the crystal.
Additionally, in the “Symmetry Elements” tab you can tick and untick the symmetry elements you want or do not want to visualize: in Figure 5, we choose to show the 3-fold screw axes (in yellow) and the corresponding arrows, which allow screw axes to be distinguished easily from the other axes.
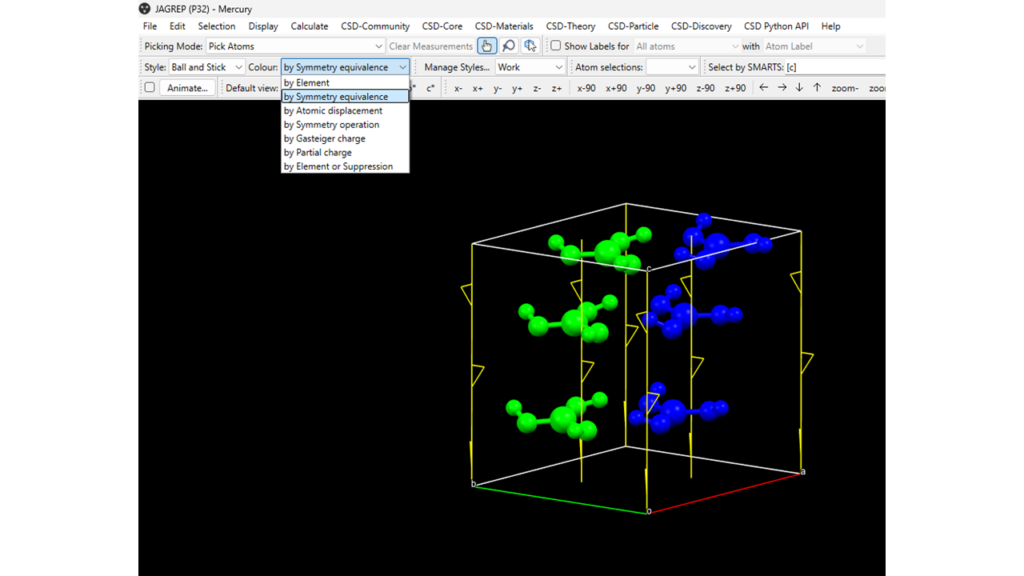
Finally, to visualize molecules that are related by crystallographic symmetry more easily, you can change the colour of visualization from “by Element” (default) to “by Symmetry equivalence” on the top left of the Mercury home tabs (Figure 6).
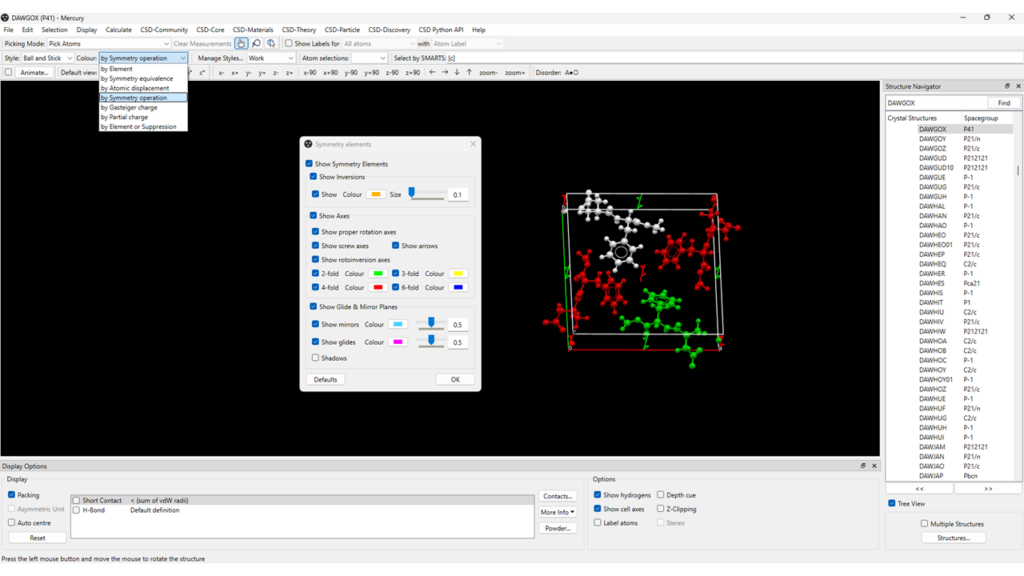
If the atoms in a structure are coloured by “Symmetry operation”, instead, each molecule or ion is coloured according to the symmetry relationship it has with the asymmetric unit (Figure 7). The latter is defined as the smallest part of a crystal structure to which symmetry operations can be applied in order to generate the complete crystal repeating unit, called unit cell.
Note that the contents of the asymmetric unit are highlighted in light grey.
Next Steps
- Watch our video “How to View Symmetry Elements and Operations in Mercury” to learn how to visualize the symmetry elements in crystal structures and how to access the list of symmetry operators in Mercury.
- Find here additional resources that can be helpful for crystallographic symmetry handling and visualization: De la Flor, G., Aroyo, M. I., Gimondi, I., Ward, S. C., Momma, K., Hanson, R. M. & Suescun, L. (2024). Free tools for crystallographic symmetry handling and visualization. J. Appl. Cryst. 57, 1618-1639.
- To discuss further and/or request a demo with one of our scientists, please contact us via this form or .